Original: http://www.columbia.edu/cu/computinghistory/hh/
H. HOLLERITH
| Od Kvartalni, Škola rudnika Columbia univerzitet, Vol. X No.16 (Apr 1889), pp.238-255. U ovom članku autor, Kolumbija diploma (Rudnici 1879) Herman Hollerith, opisuje uređaja i metoda je razvio automatizirati 1890 US Census; to je osnova za njegovu Columbia doktorat 1890 To je skeniran i pretvara u HTML Frank da Cruz Univerziteta Kolumbija u januaru 2004. godine za Projekt računarstvo Povijest Columbia Univerzitet. Originalni tekst nije promijenjen na bilo koji način (osim ako slučajno), osim da činjenica da su razbijena od strane rastavljanje su vratio. Original broja stranice su prikazani inline kao [- xx -]. Slike, fusnote, a stolovi su postavljeni kao u originalnom članku; kliknite na bilo koju sliku da vidite veću verziju. (Podaci početi na stranici 247.) Izmjene u HTML5 i za prijevode, januar 2019. |
MALO, koji nisu direktno došli u kontakt sa popisnom kancelarijom, mogu formirati bilo kakvu adekvatnu ideju o radu koji je uključen u sastavljanje popisa od 50,000,000 osoba, kao što je bio slučaj u prošlom popisu, ili preko 62,000,000, kao što će biti Međutim, činjenica da je Kongres na svojoj posljednjoj sjednici u “Aktu kojim se predviđa donošenje jedanaestog i narednih popisa” određuje maksimalni trošak za sljedeći ili jedanaesti Popis, bez štampanja i graviranja, na 6.400.000 dolara, možda će impresionirati nekoga sa idejom o veličini takvog poduhvata.
Iako je naša populacija je u stalnom porastu, pa iako na svakom popisu složenije kombinacije i podrobnije su potrebni u raznim kompilacijama, ipak, sve do sadašnjeg vremena, bitno je originalni metod kompilacije je [-239-] zaposlen; da izrade dužine-oznaka u malim trgovima, a zatim dodavanje i brojanja takve dužine-maraka.
Dok se bavila radom na desetom popisu, pažnja pisca bila je pozvana na metode korištene u tabeliranju populacijske statistike i na ogromne troškove. Ove metode su u to vrijeme opisane kao “barbarske, neke mašine treba osmisliti u svrhu olakšavanja takvih tabulatora. To je dovelo pisca do detaljnog proučavanja detalja o korištenim metodama, koje su bez sumnje bile najodgovornije ikada Nakon pažljivog razmatranja mnogih problema koji su uključeni i značajnog eksperimentisanja u velikom obimu, metod koji formira predmet ovog rada pouzdano se nudi kao sredstvo za olakšavanje ovog rada.
Rad popisa može se podijeliti u dvije glavne grane: onu popisivanja i kompilaciju ili tabeliranje. Što se tiče popisivanja, plan koji je prvobitno usvojen na desetom popisu, sa tako sjajnim rezultatima, bit će u značajnoj mjeri praćen u sljedećem popisu, a predviđen je u gore navedenom Aktu Kongresa. Kao što je prema odredbama ovog Zakona popisivači plaćeni prema broju osoba, farmi ili proizvodnih pogona nabrojanih, a kako su stope kompenzacije neznatno povećane, trošak nabrajanja po glavi stanovnika nužno mora biti neznatno veći od deseti popis. Pozivajući se na zapise desetog popisa, smatramo da je cijena popisivanja iznosila $ 2,095,563.32.*
Povećanje broja stanovnika od trideset posto. tokom decenije se može razumno pretpostaviti, tako da troškovi popisivanja na jedanaestom popisu, po istoj stopi po glavi stanovnika, ne bi bili manji od 2,724,232.32 dolara. Dodavanje na ovaj iznos troškova dodatnih rasporeda koji se zahtevaju prema ovom aktu Kongresa i omogućavanje povećanja stope naknade za popisivanje
_____________________
* Trošak desetog popisa bio je sljedeći:
| Popisivači |
$2,095,563.32 |
| Kancelarija nadzornika |
2,385,999.50 |
| Specijalni agenti |
625,067.29 |
| Štampanje izvještaja |
678,624.61 |
| Ukupno |
$5,785,254.72 |
[-240-] farmi i proizvodnih pogona,* vidimo da procjena od 3.000.000 $ nije nerazumna za troškove sljedećeg popisivanja.
Iz tako nabrojanih podataka sastavljaju se različiti izvještaji koji čine legitiman rad popisa. Troškovi ureda nadzornika Desetog popisa stanovništva u Vašingtonu iznosili su 2.385.999,50 dolara. Ako se u narednom popisu trebaju koristiti iste metode kompilacije, troškovi kompilacije po glavi stanovnika bi, naravno, ostali suštinski isti, tako da bi se omogućilo povećanje populacije, troškovi ovog dijela posla iznosili bi $ 3,101,799.67. Tome treba dodati i troškove sastavljanja dodatnih podataka koji se zahtijevaju prema aktu Kongresa. Ako, međutim, podaci nabrojani na sledećem popisu budu sastavljeni sa puninom i potpunošću koju zaslužuje i koju treba da primi, ovi troškovi bi daleko premašili gore navedeni iznos. Kao što će se sada pokazati, mnoge činjenice nabrojane u desetom popisu uopšte nisu bile sastavljene, ili ako su sastavljene, tretirane su na tako jednostavni i elementarni način da ostavljaju mnogo da se poželi. S druge strane, međutim, kompilacije desetog popisa bile su toliko superiorne u odnosu na sve što se ranije pokušavalo da se vrlo vjerovatno zaključi da deseti popis ne ostavlja ništa što bi bilo poželjno. Ako se na jedanaestom popisu ne donesu materijalna poboljšanja u metodama tabeliranja, verovatno će se smatrati nemogućim ostvariti više od desetog popisa zbog vremena i troškova.
O popisu se često govori kao o fotografiji društvenih i ekonomskih uslova jednog naroda. Analogija se može napraviti ne samo u odnosu na dobijene rezultate, već i na metode
| Popisivači |
Stope naknade |
| |
1890
Popis |
1880
Popis |
| Za svakog stanovnika nabrojenog |
2 |
2 |
| Za svaku zabilježenu smrt |
2 |
2 |
| Za svaku se farmu vratio |
15 |
10 |
| Za svaku prerađivačku industriju |
20 |
15 |
| Za svakog vojnika, mornara, itd |
5 |
…………. |
[-241-] dobijanja ovih rezultata. Na taj način popisivanje popisa odgovara izloženosti ploče u fotografiji, dok kompilacija popisa odgovara razvoju fotografske ploče. Osim ako je fotografska ploča pravilno izložena, nemoguće je dobiti dobru sliku, tako da je, u slučaju popisa, dobar rezultat nemoguć, osim ako je popisivanje izvršeno na odgovarajući način i sa dovoljno detalja. Kao što je prvi tok developera iznio istaknute tačke naše fotografske slike, tako će u slučaju popisa prvi tabelarni prikazi prikazati glavne karakteristike naše populacije. Kako se razvoj nastavlja, pojavljuje se mnoštvo ili detalj u svakom dijelu, dok se istodobno istaknute osobine ojačavaju i izoštravaju u definiciji, dajući konačno sliku punu života i snage. Takav bi bio rezultat pravilno sastavljenog i probavljenog popisa iz temeljnog popisivanja. Ako ova zemlja troši 3.000.000 dolara na izloženost ploče, zar se slika ne bi trebala pravilno razvijati?
Rasporedi stanovništva desetog popisa stanovništva sadržavali su sljedeće upite, a odgovori na njih bili su sposobni za statističku obradu:
- Rase ili boje: da li je bijela, crna, mulat, kineski ili indijski.
- Seks.
- Godine.
- Odnos svake osobe nabrojane u glavu porodice.
- Civilne ili bračne stanje: da li jedan, oženjen, udovice, ili razvedeni.
- Da li se udala u toku popisa godine.
- Zanimanje.
- Broj mjeseci nezaposlenih.
- Da li bolestan ili na drugi način privremeno onemogućeno kako bi bio u mogućnosti da prisustvuju redovnog poslovanja ili dužnosti na dan popisivanja; šta je bolest ili invaliditet?
- Da li slijepi, gluhi i glupi, idiotski, lud, osakaćeno, osakaćen, prikovana za krevet, ili na drugi način osobe s invaliditetom.
- Da li je osoba pohađala školu u toku popisa godine.
- Ne mogu čitati.
- Ne mogu pisati.
- Mjesto rođenja.
- [-242-] Mjesto rođenja oca.
- Mjesto rođenja majke.
Ovakvo popisivanje, ako je to učinjeno temeljito, svakako korespondira sa potpuno vremenskom ekspozicijom naše fotografske ploče. Teško da bi se to moglo nazvati nedovoljno izloženim.
Ako je zanimljivo i vrijedno znati broj muškaraca i žena u našoj populaciji, koliko je veći interes znati broj domaćih muškaraca i stranih muškaraca; ili opet, znati broj domaćih bijelih muškaraca, stranih bijelih muškaraca, obojenih mužjaka, itd.; ili opet, kombinacija svake od ovih činjenica sa svakom godinom starosti. Sve je to učinjeno u desetom popisu. Napravljene su mnoge druge zanimljive i vredne kombinacije, daleko nadmašivši bilo šta što se ikada prije pokušavalo, ali, s druge strane, mnoge nabrojane činjenice uopšte nisu bile sastavljene. Tako, na primer, danas je nemoguće dobiti najmanji pouzdani statistički podatak u vezi bračnih uslova naših ljudi, iako su potpuni podaci o tome zaključani u povratku popisa desetog popisa. Drugim riječima, razvoj se nije odvijao dovoljno daleko da bi se prikazao čak i ovaj najvažniji detalj naše slike. Pitanje zašto ova informacija nije sastavljena nekoliko puta je postavljano tokom rasprave o sadašnjem zakonu o popisu u odboru Senata. Tačan i pravilan odgovor na ovaj upit bi vjerojatno bio jednostavno, “nedostatak sredstava. Na minut da eminentni statističar koji je planirao i usmjerio deseti popis nije u potpunosti shvatio vrijednost takve kompilacije.”
Da znam, jednostavno je broj jedan, u braku, udovice i razvedena osoba u našem narodu će biti od velike vrijednosti, ipak bi bilo vrlo mnogo veće vrijednosti imati iste informacije u kombinaciji s godinama, sa seksom, sa rase, sa horoskop, sa zanimanjem, ili sa različitim pod-kombinacija ovih podataka. Ako podaci u pogledu odnosa svake osobe u glavu porodice su pravilno sastavljeni, u kombinaciji s raznim drugim podacima, ogromnu količinu vrijednih informacija bi se dobiti. Dakle, još jednom, ako se pravilno nabrojane broj mjeseci nezaposlenih i sastavljen u odnosu na dob, zanimanju, itd, više informacija može se dobiti od velikog [-243-] vrijednost student ekonomske probleme koji utiču na naše plaće-zarađuju.
Još jedna ilustracija će biti data. U popisu smo, pored podataka koji se odnose na naše živo stanovništvo, evidentirali smrtne slučajeve tokom prethodne godine. U oba slučaja imamo informacije o dobi i zanimanju. Žive populacije su tabelarno prikazivane kombinacijom starosti i zanimanja, a isto tako i smrti po godinama i zanimanjima, onda bismo imali podatke iz kojih bi se mogli izvući pouzdani zaključci u vezi sa efektima različitih zanimanja na dužinu života. Možda je čak moguće napraviti tablice života za različita zanimanja kao što to sada činimo za različite države i gradove. Takve informacije bi bile korisne u vezi sa životnim osiguranjem i drugim problemima. Opet. ona bi ukazala na sve potrebne reforme u vezi sa sanitarnim uslovima i okruženjem bilo kog zanimanja. Ovo je oblast statističkog istraživanja koja je još uvijek u potpunosti neistražena.
U vezi s tim možda bi bilo prikladno citirati pismo upućeno piscu, u odgovoru na određena pitanja, general Francis A. Voker, poznati nadzornik Desetog popisa:
“U popisu stanovništva tako popularne zemlje kao što je Sjedinjene Države rad na tabeliranju može se odvijati gotovo doslovno bez ograničenja, a ipak ne prestaje da dobija nove činjenice i kombinacije činjenica političkog, društvenog i ekonomskog značaja.
“Sa takvim poljem pred statističarem, to je čisto pitanje vremena i novca gde će se zaustaviti. Uopšteno govoreći, on ne može da uradi manje nego što je urađeno ranije u tretmanu iste teme. Želja da se ide nešto više od svojih prethodnika i da uvede neke nove karakteristike u interesu i uputi vlastitu izbornu jedinicu, tako da postoji stalna tendencija da se statistički tretman sličnog materijala postepeno sve više i više komplikuje. poboljšanja u statistici jedne zemlje imaju veći ekonomski značaj od nekih ranijih i elementarnijih grupacija činjenica.”
Niko nije kompetentniji da govori autoritativno o ovom pitanju nego generalu Vokeru, i svakako nijedno mišljenje nije vrednije razmotriti.
Bez obzira na želje i želje onih koji su zaduženi [-244-] naših različitih statističkih istraživanja, mi često nalazimo u ovoj zemlji da je javno mnjenje potrebama i zahtjevima pojedinih statističkih podataka. Tako je u ovom Zakonu Kongresa dok je glavni boda ostaju diskreciono sa sekretarom za unutrašnje poslove, pod čijim pravac popisu se uzima, i dalje na određene tačke direktne instrukcije daju. Na primjer, predviđeno je da se boji stanovništvo se nabrojani i tabelarno u odnosu na razlike crnaca, mulata, quadroons i octoroons. U popisu 1860 stanovnika je sastavljen ispod 14 starosnim grupama, 1870. su u dobi prebrojani ispod 25 grupa, dok je u 1880. popisu ured, u skladu sa brojnim zahtjevima iz različitih izvora, izračunavali stanovništva prema pojedinačnim godinama starosti, odluka u svim preko 100 specifikacijama.
Do sada je u popisu stanovništva i sličnim kompilacijama slijedilo u suštini jedna od dvije metode. Ili su dokumenti sačuvani u svojim odnosima, a informacije povučene tako što će se prvo grupisati činjenice, a zatim sledeće, ili su zapisi napisani na karticama ili listićima, koji se prvo sortiraju i broje prema jednoj grupi činjenice, a zatim sljedeće.
Da bismo formirali neku ideju o pitanjima koja su uključena u prvi plan, pretpostavimo da je zapis koji se odnosi na svaku osobu na sledećem popisu napisan linijom preko trake papira, i da su takve linije udaljene tačno pola inča, onda bi trebalo da uzme traku papira dugu preko 500 milja da sadrži takve zapise. Oni se moraju iznova i iznova prebacivati dok se ne postignu sve željene kombinacije. Ovo je praktično metoda koja je uslijedila u sastavljanju deseteg popisa. S druge strane, ako se koriste pisane kartice, izgledi su malo ohrabrujući. Sto komotno tankih kartica će formirati stack viši od inča.
Prema tome, u narednom popisu, ako se takve kartice koriste, to će zahtijevati stog viši od deset milja. Zamislite na trenutak nevolje i zbunjenost koja bi bila uzrokovana time što bi se nekoliko takvih kartica izgubilo. Ova metoda pojedinačnih karata korištena je u popisu stanovništva Massachusettsa 1885. godine. Korištenih 2.000.000 kartica težilo je oko 14 tona. Da su iste kartice korištene u sljedećem popisu stanovništva Sjedinjenih Država zahtijevalo bi oko 450 tona takvih kartica.
[-245-] Umjesto ovih metoda, predlaže se da se rad obavlja u najvećoj mogućoj mjeri mehaničkim putem. Da bi se to postiglo, zapisi moraju biti postavljeni u takvom obliku da ih mašina može pročitati. To se najlakše postiže probijanjem rupa u karticama ili trakama od papira, koje se tada perforacije mogu koristiti za kontrolu krugova preko elektro-magneta koji rade brojače, ili mehanizam za sortiranje, ili oboje u kombinaciji.
Koriste se kartice za snimanje odgovarajuće veličine, čije su površine podijeljene u kvadrate kvadrata, pri čemu se svakom kvadratu dodjeljuje određena vrijednost ili oznaka. Ako, na primer, treba da se napravi zapis o polu, koriste se dva kvadrata, označena tačno M i F, i, kako se zapis odnosi na muško ili žensko, odgovarajući kvadrat je probušen. Ove rupe mogu biti probijene bilo kojim običnim udarcem, rezanjem okruglog otvora, otprilike tri-šestnaestine inča u promjeru. Na sličan način se evidentiraju i drugi podaci, kao što su stanje bračnog partnera, nepismenost itd. Međutim, često se utvrđuje da se podaci moraju evidentirati sa detaljima specifikacije da bi bilo nepraktično koristiti odvojeni prostor za svaku specifikaciju. U takvim slučajevima se koristi kombinacija dva ili više rupa za označavanje svake specifikacije. Na primer, ako je poželjno da se zabeleži svaka godina starosti, koristi se dvadeset razmaka, podeljenih u dva seta od po 10, označenih, redom, od 0 do 9. Jedan set od deset razmaka koristi se za snimanje desetina godina godine, dok se drugi set koristi za evidentiranje jedinica godina starosti. Dakle, dvanaest godina bi se zabilježilo probijanjem I u prvom setu, i 2 u drugom; dok bi 21 godina bilo zabeleženo probijanjem 2 u prvom setu, a 1 u drugom setu. Zanimanja se mogu rasporediti u proizvoljne grupe, pri čemu se svaka takva grupa označava velikim slovom, a svako posebno zanimanje te grupe malim slovom. Prema tome, Aa bi označio jedno zanimanje, Ab drugo, itd. Ako se želi, mogu se koristiti kombinacije dva ili više slova istog skupa. Dakle, AB se može koristiti za označavanje jednog zanimanja, AC drugog I BC-a, itd. Sa takvim aranžmanom, početno slovo se može koristiti za označavanje grupa zanimanja kao i ranije. Na ovaj način je očigledno da će vrlo mala kartica biti dovoljna za elaborirani zapis. Za rad na popisu, kartica 3″× 5½” bila bi dovoljna da odgovori na sve uobičajene svrhe. Kartice su poželjno izrađene od tankog materijala kao što je to prikladno za rukovanje.
Ako se koriste štampane kartice, probijanje se može uraditi sa običnim karata udaraca; [-246-] više zadovoljavajuće rezultate, međutim, može se dobiti s udarcima dizajniran posebno za ovaj posao, kao što će biti sada opisan.
U popisu, popisni okrug formira statističku jedinicu površine, a pogodna kombinacija je uređena tako da odredi svaku takvu oblast. Kartica je probijena odgovarajućom kombinacijom za svaku osobu u takvim popisnim krugovima, a kartice svakog okruga se zatim numeriraju uzastopno, u odgovarajućoj mašini za numerisanje, da bi odgovarale brojevima dodijeljenim pojedinačnim zapisima na popisivačima. Ova kombinacija rupa i ovog broja služiće za identifikaciju bilo koje kartice. Ako se bilo koja kartica izgubi, lako je otkriti među brojem karata time što jedna ili više rupa neće odgovarati rupama u bilansu karata. Pomoću odgovarajuće žice ili igle može se testirati snop od hiljadu ili više kartica u nekoliko sekundi, i otkriti sve zagubljene kartice. Kada se zapamti da se u popisu mora stalno baviti milijunima kartica, cijeni se važnost ovog razmatranja. Sa običnim pisanim karticama bilo bi praktično nemoguće otkriti pogrešno postavljene kartice, a nekoliko takvih pogrešno postavljenih kartica bi izazvalo gotovo beskrajnu konfuziju.
Budući da su kombinacije rupa koje se koriste za označavanje okruga popisivača iste za sve kartice tog okruga, uređen je poseban stroj za probijanje ovih rupa. Ova mašina je opremljena brojnim međusobno izmjenjivim bušilicama, koje su postavljene u skladu sa kombinacijom i željeno je probiti. Pet ili šest karata se zatim stavljaju u proboj na odgovarajuće pregrade, a pomoću poluge se odgovarajućim rupama probijaju ove kartice u jednoj operaciji.
Pojedinačnih evidencija sada prepisuju sa odgovarajućim karticama udarati po unaprijed pripremljene sheme kao što je opisano gore. Za tu svrhu ono može biti poznat kao tastatura-udarac je uređen, u kojoj je kartica se održava fiksiran u okvir, dok je udarac se preselio preko kartice u bilo kojem smjeru pomoću projektovanje poluge dobili odgovarajuće dugme ili rukovanje . Ispod dugme je tastatura pruža sa rupama slovima i brojevima prema dijagramu kartice, i tako uređen da kada pin projektovanje ispod dugmeta je preko bilo rupe, udarac je završen odgovarajući prostor kartice. Ako je pin depresiji u bilo rupa od tastature, udarac upravlja i odgovarajuće [-247-] prostor kartice je udario. Sa takvim tastature udarac to je, naravno, jasno da je savršeno prazna kartica se može koristiti,
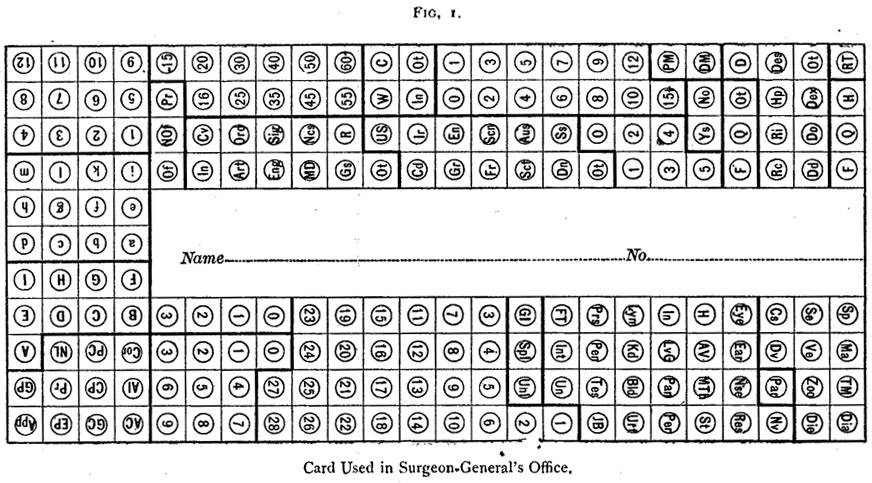
međutim, jedan ugao se prekida kako bi se kartica pravilno locirala u narednim operacijama.
Da biste pročitali takav udario kartona, potrebno je samo da se [-248-] stavite ga preko štampanom obliku, po mogućnosti različite boje, kada je kompletan zapis prikazuje direktno kroz rupe.
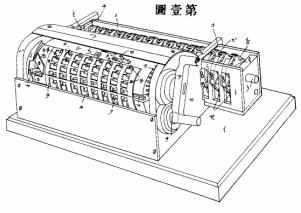
Do sada se samo upućivalo na kompilaciju popisa, ali su te metode podjednako primjenjive na mnoge druge oblike statističkih kompilacija, kao što su, na primjer, različiti oblici vitalne statistike. Slika 1, na primer, predstavlja dijagram kartice koji se trenutno koristi u kancelariji generalnog hirurga SAD-a, za sastavljanje vojne zdravstvene statistike. Podaci koji se odnose na mjesec, poziciju, podjelu i regiju na koju se zapis odnosi, bilježe se probijanjem rupe u svakoj podjeli preko kraja kartice pomoću stroja s izmjenjivim udarcima kao što je prije opisano. Ovaj deo
zapis se gotovo tačno poklapa sa zapisom popisa za popisivanje. Pojedinačni zapis se zatim prepisuje na karticu tako što se probija u preostale prostore pomoću tastature-bušenja kao što je ranije opisano.
Takva kartica omogućava kompletnu evidenciju, uključujući sljedeće podatke za svaki pojedinačni; rang, ruka usluga, dob, rasu, nacionalnost, dužina radnog staža, dužina boravka na određenom post, da li je bolest ugovorena je u dužnosti ili ne, da li je priznao da je bolestan izvještaj u toku mjeseca ili u toku prethodnog meseca, izvor prijema, raspored predmeta, odnosno da li preostale pod terapijom, mjesto liječenja, bolesti ili povrede za koje tretiraju, i na kraju tretira broj dana. Između 40.000 i 50.000 takvih evidencija se dobila [-249-] godišnje, a iz ovih se sastavljaju razne zdravstvene statistike koje se odnose na našu vojsku.
Kartica je upravo uređen za Odbor za zdravstvo Njujorka koji se koristi u izradi statistike smrtnosti tog grada. Rekord za svaku smrt dešavaju u gradu Njujorku, kao što je dobila od certifikate liječnika, je prepisan na takvu karticu udaraju kao i ranije opisani način. Ova kartica omogućava snimanje sljedeće podatke: spol, dob, rasu, bračne stanje,
zanimanje, rodno mesto, rodno mesto roditelja, dužina boravka u gradu; odjeljenje u kojem je nastupila smrt, sanitarna podjela takvog odjeljenja, priroda prebivališta u kojem se smrt dogodila, da li je to stan, stan, hotel, javna ustanova, itd., i na kraju uzrok smrti. U gradu Njujorku godišnje se bilježi oko 40.000 smrtnih slučajeva.
Ove ilustracije će poslužiti da pokažu kako se kartica može spremiti za snimanje gotovo svih željenih grupa činjenica.
Uz malu praksu osigurana je velika stručnost u izradi takvih transkripcija, pa se zapis može prepisati mnogo lakše nego pisanjem, čak i ako je napravljena znatna odredba za olakšavanje pisanja upotrebom skraćenica.
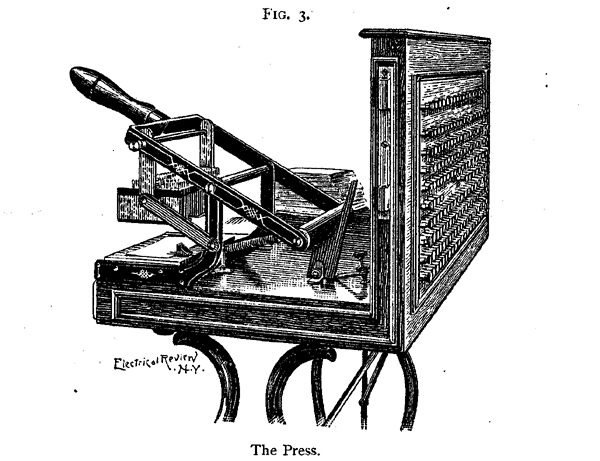
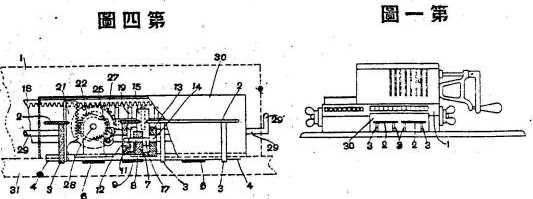
Od udario kartona je pored postaje neophodno [-250-] sastaviti željeni statistike. U tu svrhu aparat prikazan na slikama. 2 do 8 se koristi. Štampe ili kola-zatvaranje uređaja, koji je prikazan na slikama. 2, 3 i 4, sastoji se od tvrde gume krevet ploča, kao što je prikazano u poglavlju u Sl. 4, pod uslovom da sa odgovarajućim zaustavljanja ili pokazivači protiv kojih rekordno kartice mogu se postaviti. Ovo tvrde gume ploča je opremljena broj rupa ili čaše odgovarajući u broju i relativni položaj s centrima
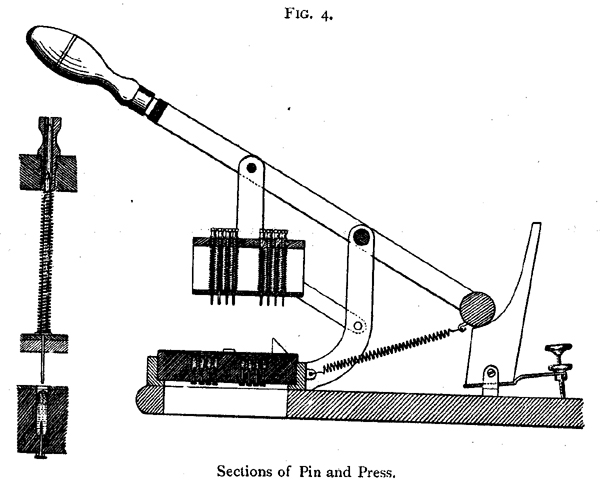
prostori kartice. Gvozdene žice noktiju je sigurno prešao kroz rupu u dnu svake kup, i žice, povezivanje na svom drugom kraju sa obavezujući post na poleđini štampe okvira, čvrsto održava pod glavu svakog nokta. Svaki kup je djelomično ispunjena živom, koji, kroz nokat i žice, stoga u električnoj vezi sa odgovarajućim vezivanja-post. Iznad tvrde gume ploča je klipni predviđenu kućicu sa brojnim projektovanje opruge aktivira poena, odgovarajući na broj i raspored sa centrima žive čaše. Izgradnju i uređenje ovih igle je prikazan na sl. 4. Ako je kartica postavljena na gumene ploče protiv zaustavljanja je naravno jasno da, kada je kutija oboren za ručicu, igle će sve biti pritisne natrag , osim kao što odgovaraju [-251-] sa udario prostore karticu koja projektuju u živu, i stoga su u električni priključak sa odgovarajućim vezivanja-poruke na leđa štampe okvira.
Jedan broj mehaničkih brojila su raspoređeni u odgovarajući okvir, kao što je prikazano na sl. 5. Lice svakog kontra je tri inča kvadratnih, a dobija se uz dial podijeljen u 100 dijelova i dvije ruke, jedna brojne jedinice druge stotine. Brojač se sastoji uglavnom od elektro-magnet, armatura od kojih je tako uređen da svaki put kada se privukla zatvaranjem
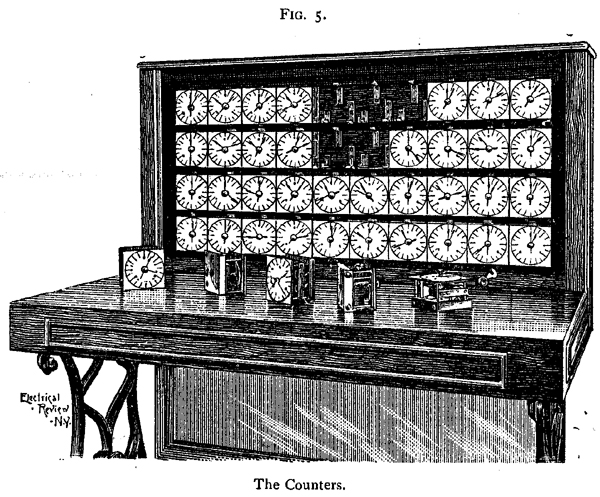
kolo registruje jedan. Odgovarajući nošenje uređaja je uređen tako da se u svakom potpunu revoluciju jedinice ruke stotinu ruku registruje jedan, svaka kontra pa se tako i brojanje do sto sto, ili 10.000, koja će se naći dovoljno za sve obične statističke svrhe. Šalterima su tako raspoređeni da oni mogu lako se resetirati na 0, a svi se skidaju i izmjenjivim, sama postavljanje brojača na poziciju u okviru donošenja potrebnih električnih priključaka kroz magnet.
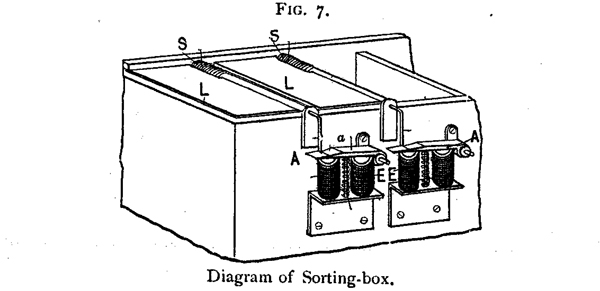
Za potrebe sortiranja kartica po bilo koju grupu [-252-] statističkih predmeta ili kombinacija dva ili više takvih stavki, sortiranje-box, koji je prikazan na sl. 6, koristi. On se sastoji od kutije odgovarajuće podijeljeni u pregrade, od kojih je svaka zatvorena poklopcem. Svaki poklopac, L, kao što je prikazano na sl. 7, održava zatvorena protiv napetosti opruge, S, koje je ulov, a, u armaturu, A. Ako je krug zatvoren kroz magnet, E, armature, A, je
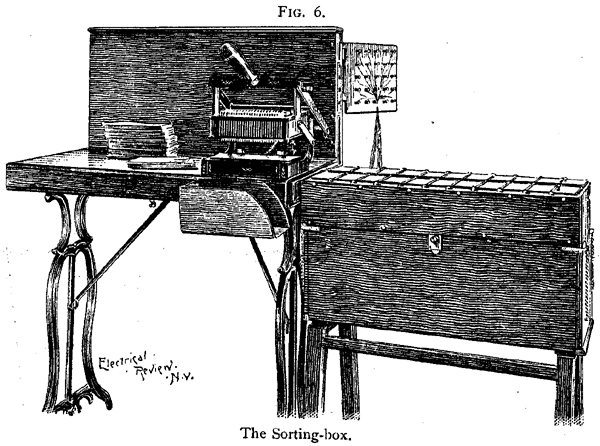
privukao i na taj način oslobađaju poklopac, L, koji je otvoren do izvora, i ostaje otvorena do ponovo zatvoren rukom.
Kako se udario kartice su raspoređeni po okruzima popisivača “, koji čine naš jedinici površine. Prva kompilacija koja bi se željena bi dobiti statistike za svakog popisnog kruga prema nekim nekoliko kondenzirane grupacijama činjenica. Tako bi se moglo željeni znati broj muškaraca i žena, od native rođen i stranih rođeni, bijelaca i boji, sa jednim, oženjen, i udovice, broj na svakoj od grupa centra dobi, itd, u svakom popisnog kruga. Da bi se dobila takvu statistiku odgovarajući obavezujući-poruke na poleđini štampe okvira su povezani putem pogodan komad pokrivena žice, sa vezivanja postova od šaltera na kojima se želi da registruje odgovarajuće činjenice. Odgovarajuća baterija se raspoređenih u krug, jasno je da ako je kartica se stavlja na [-253-] čvrsti gumeni ležaj ploča, a kutijicu štampe srušen na karticu, igle odgovara sa udario prostorima će se zatvoriti krug kroz magnete odgovarajućeg brojača koji na taj način registruju po jedan. Ako su brojači prvi postavljena na 0, a kartice date popisnog kruga tada je prošao kroz pritisnite jedan po jedan, broj muškaraca i žena, bijelaca i boji, itd, će biti naznačeno na odgovarajućim šalterima.
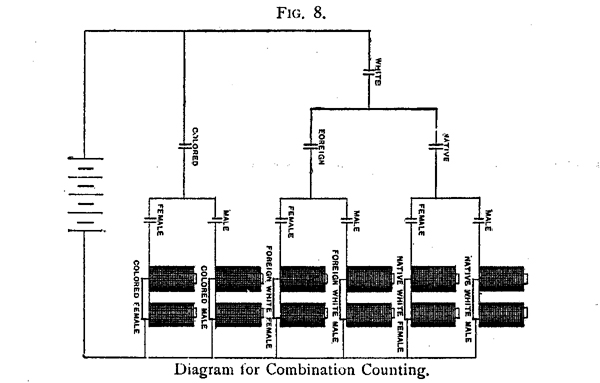
Ako se želi računati direktno na brojače, kombinacije dva ili više predmeta, mali releji se koriste za kontrolu sekundarnih krugova preko brojača. Ako je, na primjer, poželjno znati broj autohtonih bijelih mužjaka, prirodnih bijelih ženki, stranih bijelih mužjaka, stranih bijelih ženki, obojenih mužjaka. i obojenih ženki; to su kombinacije pola, rase i rođenja, obični releji su raspoređeni kako je prikazano na dijagramu, sl. 8, čiji su magneti povezani sa štampom kako je naznačeno. Ako je kartica utisnuta za prirodni bijeli, a muški postavljen u prešu, pokreću se odgovarajući releji, koji zatvaraju sekundarni krug preko magneta brojača, izvorni bijeli mužjak, te tako registruju jedan na odgovarajući brojač.
Odgovarajućim rasporedom releja može se računati svaka moguća kombinacija podataka snimljenih na karticama. Međutim, kada se želi računati sa složenijim kombinacijama, koriste se posebni releji sa višestrukim kontaktnim tačkama.
Ako se želi asortiman ili distribuiraju kartice prema bilo željenu stavku ili kombinacije stavki snimljene na kartici, samo je potrebno povezati magneta za sortiranje kutije na potpuno isti način kao što je to opisano za brojače. Kada se kartica se zatim stavlja u novinama, jedan od poklopaca za sortiranje kutije, prema podacima snimljene na kartici, će se otvoriti. [-254-] kartica se odlaže na otvorenom pregradi sortiranje kutije i poklopac zatvoren s desne strane, dok je u isto vrijeme naredne kartica se stavlja u položaj u štampi sa lijevom rukom.
To je, naravno, jasno da je bilo koji broj predmeta ili kombinacija predmeta može računati. Broj takvih predmeta ili kombinacija, koja se može računati u svakom trenutku, koji su ograničeni samo po broju brojila, dok u isto vrijeme karte su poredani po bilo koju željenu skup statističkih činjenica. U popisu iz kartice kao oni dolaze iz probijanje će, naravno, biti raspoređeni po popisnim krugovima.
Svaka distrikta bi se tada mogla voditi kroz štampu, a činjenice koje se žele znati u vezi sa ovom jedinicom područja mogu se računati na šalterima, dok su kartice istovremeno raspoređene prema nekom drugom nizu činjenica, raspoređivanje u prikladnom obliku za dalje tabeliranje. Na ovaj način, rasporedom razborite “šeme”, naći će se da se najsloženija kompilacija može izvršiti samo sa nekoliko obrada karata.
Dva od najvažnijih elemenata, u gotovo svim statističkim kompilacije, su “time što rezultati mogu se dobiti sa ovim metodom, u popisu, na primjer, biti zavisi od: 1., stopa po kojoj službenik mogao udariti rekord -cards, i, 2d, broj službenika zaposlenih na ovom dijelu posla. Prvi se lako može odrediti eksperimentom, kada je drugi postaje samo [-255-] jednostavan aritmetičke proračun. Rad brojanje ili tabelarno na mašinama može se tako urediti da, u roku od nekoliko sati nakon posljednje kartice za bateriju, prvi set stolova, uključujući kondenzirane grupisanje svih vodećih statističke činjenice, ne bi bio potpun. Brzine kojom bi mogao biti objavljen kasnijim tablicama bi ovisilo samo o broju mašina zaposlenih.
Što se tiče tačnosti, očigledno je da se procesi brojanja i sortiranja, koji su čisto mehanički, mogu s takvim provjerama urediti da je greška praktično nemoguća. Jedan mogući izvor greške je u probijanju karata. Ako se poduzmu odgovarajuće mjere opreza, može se dobiti popis koji je praktično bez grešaka u kompilaciji. Čak iu ovom pogledu sadašnji metod bi imao očigledne prednosti. Kartica koja je pogrešno probijena može uključivati grešku samo jedne jedinice, dok su pri svim prethodnim metodama moguće pojedinačne greške koje uključuju grešku kao rezultat desetaka, stotina, tisuća ili čak i više.
Čvrsto se vjeruje da će, s obzirom na troškove, vrijeme i točnost, ova metoda imati veoma velike prednosti u obavljanju posla koji je do sada obavljen, ali se vjeruje da je to beznačajno u odnosu na činjenicu da bi bila moguća temeljna kompilacija, u razumnim granicama troškova, dok je takva kompilacija praktično nemoguća, uobičajenim metodama, zbog ogromnih troškova.
Frank da Cruz
Kineski 
Roichi Yazu (1874-1905) je bio vrlo pametan izumitelj na mnogim poljima u rasponu od rječnika do aviona. Godine 1902. izumio je mehanički računske mašine i patent je odobren da ga u 1903. Ovaj stroj je neka vrsta hibrida između vrsta pinwheel i Soroban. Godine 1902. on je ugradio kompanija Yazu Jido Soroban (Yazu Automatska Soroban) u Tokiju. Mašina je imenovan Patentirani Yazu Arithmometer, a 200 jedinice su proizvedeni. Međutim, on je ispustio projekta kada je odlučio da izgradi avion sa opremljenom motorom. On je uložio sav svoj novac u ovom projektu.
Kada je preminuo, njegov otac je pokušao da se poboljša mašinu, ali nije imao uspjeha sa poslovnim. Niko se svoje kalkulator.
Ko je napravio ovaj stroj? To je još uvijek misterija. Maruzen prodao mašinu oko 1.921. Maruzen je poznati izdavač knjiga i Business Machines i stacionarne distributer u Japanu. Maruzen prodao Brunsviga, Muldivo, milionera i Marchant mašine prije ideal.
Ohmoto Torajirou osnovana Ohmoto Tekko (a metala tvornica) u Osaki. Ova kompanija je imao mnogo vrsta metala djela kao što nas slikati limenke, sefova i održavanje poslovnih mašina. On je završio svoj prvi računske mašine, Tiger, u informacijama 1923. Službenom kompanija navodi da je on to izmislio, nakon nekoliko godina napornog rada. Ali ja sa žaljenjem reći da izgleda kao imitacija 
Tiger je postala najveća mehanička računanje proizvodnju zabrinutost u Japanu.Njegova viši direktor prodaje studirao u SAD-u, u organizaciji sistema prodaje po uzoru na Nacionalni kasa. Ovo je uključivalo direktne prodaje, život garancija, dobro održavanje, popraviti cijene (bez popusta) i dobro obučeni prodajne sile. Oni proizvode oko 
Ikuzo Ochi ugraditi Taiyo Proračun Machine Co, Ltd u Osaki 1934. On izmakne iz Tiger i pokrenuli modele “Aikoku” i “Taiyo.” Njihova nosivost sistem izgleda kao onaj u Britannic.
Maruzen spojio sa Taiyo 1939. godine i ugrađeni Maruzen Proračun Machine Co, Ltd. koji je kasnije preimenovan u Maruzen Jimukikai (business machine) & Co, Ltd. Maruzen dobili naredbu za velike brzine izračunavanje strojeve iz japanske vojske, ali to nikada nije ispunjeno.
Nippon Proračun Machine Co, Ltd. je osnovalo Showa Yoko 1945. godine. Možda su kupili zaštitni znak “Fuji Boshi ” iz K. Hirata koji žig registrovan nakon što je spin iz Tiger.
Oni su pokrenuli Fuji Boshi, SM-1 i HL-21. Neki Mašine nose i ime Busicom.
Ikuzo Ochi se ponovo ugraditi Taiyo 1951. godine nakon što je Maruzen prodao svoje fabrike mašina za računanje. Taiyo je podružnica Uchida Youkou Co, Ltd oko 1955. Uchida Youkou je distributer poslovni prostor opreme.
Blue Star je napravljen od Tokyo Electric Co, Ltd, koja je sestrinska firma Toshiba. Rani model (u crnoj i boji) je prodao Nippon Jimuki Co, Ltd u 1951. Ovaj model je bio kopija 
, Ne znam je proizvođač ovog aparata. Jednom univerzitetu kaže da je ovaj stroj napravljen je Corona Proračun Machine Co, Sjedinjene Američke Države, ali ja ne znam takva kompanija u SAD-u.Vidio sam jedan oglas u novinama koji kaže “Corona Proračun Machine je najbolji stroj napravljen u Japanu.”
Keybar Proračun Machine Co, Ltd je osnovana 1957. Izgleda da su imitirali Brunsviga Model 10. Keybar Model A-1 (1957?)
Četiri bube stoje na četiri ugla kvadrata. Oni su gladni (ili usamljeni) i na istom trenutku svaki od njih vidi bug na sljedećem uglu preko i početi puzeći prema njemu. Šta se dešava?
, beskonačnu kaskada korijena.
, beskonačnu kaskadu frakcija.
