Četiri boje teorema – the-sciences

Source: http://people.math.gatech.edu/~thomas/FC/fourcolor.html

Ova stranica daje kratak pregled novog dokaza o četiri boje teorem i četiri-bojanje algoritam pronašao Neil Robertson, Daniel P. Sanders, Paul Seymour i Robin Thomas.

Sadržaj:

Istorija.

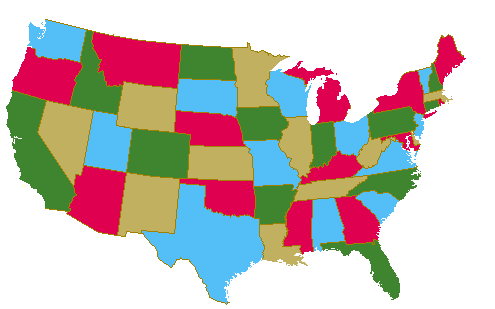
Problema Četiri Boje datira iz 1852 kada je Francis Guthrie, dok je pokušavao da obojiti kartu okruga Engleske primijetio da četiri boje dovoljan. On je zatražio od brata Frederick da li je istina da je bilo karta može biti u boji pomoću četiri boje na takav način da se susjedna područja (i.e. oni dijele zajedničku granicu segmentu, ne samo bod) dobijaju različite boje. Frederick Guthrie onda komunicirao je nagađanja da DeMorgan. Prvi štampani referenca je zbog Cayley 1878. godine.

Godinu dana kasnije prvi ‘dokaz’ Kempe pojavio; svoje neispravnost je istakao Heawood 11 godina kasnije. Drugi nije dokaz je zbog Tait 1880.; jaz u argument je istakao Petersen u 1891. Oba nisu dokazi da li imaju neku vrijednost, iako. Kempe je otkrio ono što je postalo poznato kao Kempe lanaca, i Tait pronašao ekvivalent formulacija četiri boje teorema u smislu 3-ruba-bojanje.

Sledeći veliki doprinos došao od Birkhof čiji je rad dozvoljen Franklin 1922. dokazati da je boja pretpostavka četiri važi i za mape s najviše 25 regija. Također je koristio drugi matematičari da razne oblike napredak o problemu četiri boje. Trebalo bi posebno spomenuti Heesch koji je razvio dva glavna sastojka potrebna za konačni dokaz – reducibilnosti i pražnjenja. Iako je koncept reducibilnosti je studirao od strane drugih istraživača, kao i, čini se da je ideja pražnjenja, od ključne važnosti za neminovnost dio dokaza, je zbog Heesch, i da je on bio taj koji pretpostavili da odgovarajući razvoj ove metode bi riješiti četiri boje problem.

To je potvrdio i Appel i Haken 1976., kada su objavili dokaz o četiri boje teorem [1,2].

Zašto je novi dokaz?

Postoje dva razloga zašto je Appel-Haken dokaz nije u potpunosti zadovoljavajući.

Dio Appel-Haken dokaz koristi kompjuter, i ne može potvrditi rukom, i
čak i dio koji je navodno ručno čekovni je izuzetno komplikovana i dosadan, a koliko nam je poznato, nitko nije potvrđen je u cijelosti.

Imamo zapravo pokušao provjeriti Appel-Haken dokaz, ali je ubrzo odustao. Provjera računar dijelu ne bi samo zahtijeva puno programiranja, ali i unosite opise 1476 grafikone, a da nije ni najkontroverzniji dio dokaza.

Odlučili smo da bi bilo isplativije raditi iz vlastitog dokaz. Tako smo i došli do dokaza i algoritam koji su opisani u nastavku.

Nacrt dokaz.

Osnovna ideja dokaz je isti kao Appel i Haken-a. Mi pokazuju set 633 “konfiguracije”, i dokazati svaki od njih je “svesti”. Ovo je tehnički koncept koji podrazumijeva da nema konfiguraciju sa ove nekretnine može se pojaviti u minimalnom protivprimer u četiri boje teorem. To se može koristiti u algoritam, jer ako se svesti konfiguraciju pojavljuje u planarne graf G, onda se može izgraditi u konstantnom vremenu manjem planarne graf G ‘tako da bilo koja četiri-bojanje G’ se može pretvoriti u četiri bojanje G u linearnom vremenu.

Poznato je od 1913. da je svaki minimalne protivprimer u četiri boje teorem je interno 6 povezan triangulacije. U drugom dijelu dokaz smo dokazati da je barem jedan od naših 633 konfiguracije pojavljuje u svakom interno 6 povezanih planarne triangulacija (ne nužno minimalnu protivprimer na 4CT). To se zove dokazuje neminovnost, i koristi “pražnjenja način”, prvi predložio Heesch. Evo naša metoda razlikuje se od Appel i Haken.

Glavne karakteristike našeg dokazivanja.

Mi smo potvrdili pretpostavke o Heesch da u dokazivanju neminovnost, a svodi konfiguracije mogu se naći u drugom naselju u “naplatio” Vertex; ovo je kako izbjeći “potapanje” Problemi koji su bili glavni izvor komplikacija za Appel i Haken. Naš nezaobilazni set ima veličinu 633 u odnosu na set 1476 član Appel i Haken, a naša metoda pražnjenja koristi samo 32 pravila pražnjenje, umjesto 300+ od Appel i Haken. Konačno, dobijamo kvadratnu algoritam za četiri boje planarni grafovi (opisano kasnije), što je napredak u odnosu na četvrtog algoritam Appel i Haken.

Konfiguracije.

A u blizini-triangulacije je ne-null povezani loopless avion grafikon tako da svaki konačan regija je trokut. Konfiguracija K se sastoji od gotovo triangulacije G i kartu g od V (G) na cijele brojeve sa sljedećim svojstvima:

za svaki vrh v, G \ v ima najviše dvije komponente, a ako postoje dva, onda stepen v je g (v) -2,
za svaki vrh v, ako v nije incident sa beskonačnim regiji, onda G (v) jednak stepen v, i inače G (v) je veći od stepena v; au oba slučaja G (v)> 4,
K ima prsten veličine najmanje 2, gdje se definira prsten veličine K biti zbir G (v) -deg (v) -1, sažeti u odnosu na sve čvorove u incident sa beskonačnim regiji tako da G \ v je povezan.

Prilikom izrade slike konfiguracije koristimo konvenciju uveo Heesch. Oblici čvorova ukazuju na vrijednost g (v) kako slijedi: A solid crni krug znači g (v) = 5, tačku (ili ono što se pojavljuje u sliku bez simbola na sve) znači g (v) = 6, šuplje krug znači g (v) = 7, šuplji kvadrat znači g (v) = 8, trokut znači G (v) = 9, i Pentagona znači G (v) = 10. (Ne treba nam vrhova v sa G (v)> 11, a samo jedan Vertex sa G (v) = 11, za koje mi ne koristimo nikakve posebne simbol.) Na slici ispod 17 naših 633 svesti konfiguracije se prikazuju pomoću naznačeno konvencije. Čitav set se može pogledati klikom ovdje. (Mi se odnose na (3.2) od naših papira [7] za značenje “debelih rubova” i “polu-rubova” u te slike.)

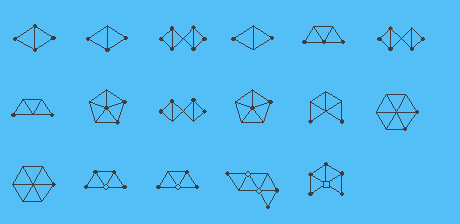
Bilo konfiguraciju kompatibilnim s jednom od 633 konfiguracije izložene u [7] se zove dobar konfiguraciju. Neka T biti triangulacije. Konfiguracija K = (G, G) se pojavljuje u T ako G je inducirana podgraf T, svaki konačan regija G je region T, i G (v) jednak stepen v u T za svaki vrh v G . Mi smo dokazati sljedeće dvije izjave.

Teorem 1. Ako T je minimalna protivprimer u četiri boje teorem, onda nije dobro konfiguracije pojavljuje u T.

Teorem 2. Za svaku interno 6 povezanih triangulacije T, neke dobre konfiguracije pojavljuje u T.

Iz navedenog dva teoreme slijedi da nema minimalne protivprimer postoji, i tako je 4CT je istina. Prvi dokaz je potreban kompjuter. Drugi se može provjeriti ručno u nekoliko mjeseci, ili, koristeći računalo, može se provjeriti oko 20 minuta.

Pražnjenja pravila.

Neka je T interno 6 povezan triangulacije. U početku, svaki vrh v je dodijeljen zadužen za 10 (6-stepeni (v)). To slijedi iz Eulerova formula koja je zbir optužbi svih vrhova je 120; Konkretno, to je pozitivno. Sada redistribuirati i naknade u skladu sa sljedećim pravilima, kao što slijedi. Kad god T ima podgraf kompatibilnim s jednom od grafikona na slici ispod zadovoljavaju specifikacije stepen (za tjeme V pravilo s negativnim predznakom pored v to znači da je stepen odgovarajuće tjemena T je najviše vrijednosti navedeno u obliku v, i analogno za čvorova sa znakom plus pored njih; jednakost je potreban za čvorove bez znaka pored njih) je zadužen za jedan (dva u slučaju prvo pravilo) treba poslati uz rub označen strelicom.

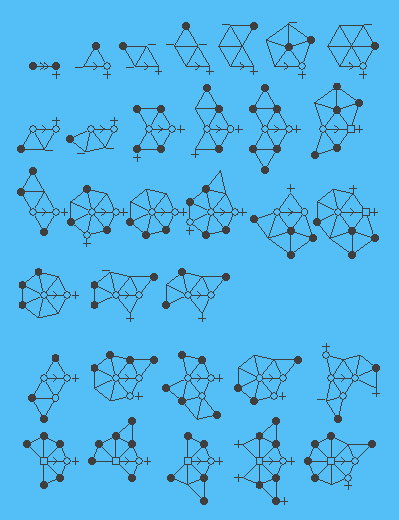
Ovaj postupak definira novi set naknada sa istim ukupnog iznosa. S obzirom da je ukupna suma je pozitivan, postoji temena v u T čija je nova zadužen je pozitivan. Mi smo pokazali da je dobra konfiguracija se pojavljuje u drugom naselju v.

Ako se stupanj v je najviše 6 ili barem 12, onda se to može vidjeti prilično lako direktnim argument. Za preostalih slučajeva, međutim, dokaza su mnogo kompliciranije. Stoga, smo pisali dokaze u formalnom jeziku, tako da se mogu provjeriti na računaru. Svaki pojedinac korak od tih dokaza je ljudski-provjerljive, ali sami dokazi nisu baš čekovni rukom, zbog svoje dužine.

Pokazivači.

Teorijski dio našeg dokazivanja opisano u [7]. Istraživanje 10-stranica je dostupna on-line. kompjuterskih podataka i programa koji se koriste u koji se nalazi na anonimnom FTP server, ali taj server je ukinut. Isti datoteke su sada dostupni iz http://www.math.gatech.edu/~thomas/OLDFTP/four/ i mogu se jednostavno pregledane. Nezavisni skup programa je napisao Gasper Fijavz pod vodstvom Bojana Mohar.

Kvadratna algoritam.

Ulaz u algoritam će biti avion triangulacije G s n vrhova. (Ovo je bez gubitka općenitosti, kao i svaka planarna grafikona može se triangulated u linearnom vremenu.) Izlaz će biti bojenje od temena G sa četiri boje.

Ako G ima najviše četiri temena obojiti svaki čvor različite boje. U suprotnom, ako G ima tjeme x stepena k <5, zatim krug C oko njega je `k-prsten ‘. Idite na analizu k-prsten ispod. U suprotnom G ima minimalan stepen pet. Za svaki vrh smo izračunati svoju snagu kao što je gore objašnjeno, i naći temena V pozitivan naboj. To slijedi iz naše dokaz Teorema 2 da bilo dobro konfiguraciju pojavljuje u drugom naselju v (to kom slučaju se može naći u linearnom vremenu), ili k-prsten krši definiciju interne 6-veza može se naći u linearnom vremenu. U ovom drugom slučaju idemo na analizu k-prsten ispod, u prvom slučaju primjenjujemo rekurzije na određeni manji graf. A četiri-bojanje G onda mogu biti izgrađeni od četiri-bojenje ovaj manji grafikona u linearnom vremenu.

S obzirom na k-prsten R krši definiciju interne 6-priključak postupak razvio Birkhof mogu se koristiti. Mi se odnose rekurzije dva pažljivo odabrana podgrafove G. A četiri-bojanje G onda mogu biti izgrađeni od četiri boje u dva manja grafikona u linearnom vremenu.

Diskusija.

Treba napomenuti da su naši programi koriste samo cijeli aritmetike, pa ne moramo biti zabrinuti sa povratno off greške i slične opasnosti od floating point aritmetike. Međutim, argument može biti da je naš ‘dokaz’ nije dokaz u tradicionalnom smislu, jer sadrži korake koji nikada ne može biti potvrđen od strane ljudi. Konkretno, nismo dokazali ispravnost kompajler smo sastavili naše programe, niti smo dokazali nepogrešivost hardvera smo ran naše programe na. Ovi se moraju uzeti u vjeri, i da su ubjedljivo izvor pogreške. Međutim, iz praktičnih gledišta, šanse kompjuter greška koja se pojavljuje stalno na isti način na sve staze naših programa na svim kompajlera u svim operativnim sistemima da su naši programi rade na je beskonačno mala u odnosu na priliku da ljudske greške u istom iznosu od slučaja provjere. Osim ove hipotetičke mogućnosti računara dosljedno daje pogrešan odgovor, ostatak naših dokaza može se provjeriti na isti način kao i tradicionalne matematičke dokaze. Mi priznaju, međutim, da provjere je kompjuterski program je mnogo teže nego provjera matematički dokaz iste dužine.

Priznanja.

Mi smo zadužili da Thomas Fowler, Christopher Carl Hekman i Barrett Zidovi za njihovu pomoć u pripremi ove stranice. Naš rad je djelomično podržan od strane National Science Foundation.

Reference.

K. Appel i W. Haken, “Svaki planarna karta je četiri colorable”. Dio I. pražnjenja Illinois J. Math. 21 (1977), 429-490.
K. Appel, W. Haken i J. Koch, “Svaki planarna karta je četiri colorable”. Dio II. Reducibilnosti, Illinois J. Math. 21 (1977), 491–567.
K. Appel i W. Haken, “Svaki planarna karta je četiri colorable”, Suvremene matematike. 98 (1989).
G. D. Birkof, “Reducibilnosti karata”, Amer. J. Math. 35 (1913), 114-128.
H. Heesch, “Untersuchungen zum Vierfarbenproblem”, Hochschulskriptum 810 / A / B, Bibliographisches Institut, Mannheim 1969.
A. B. Kempe, “Na geografski problem četiri boje”, Amer. J. Math., 2 (1879), 193-200.
N. Robertson, D. P. Sanders, P. D. Seymour i R. Thomas, “Teorema četiri boje”, J. kombiniraju. Teorija Ser. B. 70 (1997), 2-44.
N. Robertson, D. P. Sanders, P. D. Seymour i R. Thomas, Novi dokaz teorema četiri boje, Electron. Res. Objavljuje JAVNI OGL. Amer. Math. Soc. 2 (1996), 17-25 (elektronski).
T.L. Saaty, “Trinaest šarene varijacije na Guthrie je pretpostavka četiri boje”, Amer. Math. Mjesečna 79 (1972), 2-43.
T.L. Saaty i P. C. Kainen, “Problem četiri boje”. Napadi i osvajanja, Dover Publications, New York 1986. godine.
P. G. Tait, “Napomena o teorema u geometriji položaja”, Trans. Roy. Soc. Edinburgh 29 (1880), 657-660.
H. Whitney i W. T. Tutte, “Kempe lanaca i boju problem četiri”, u studije u teorija grafova, Part II (ur. D. R. Fulkerson), Math. Prof. Amerike, 1975, 378-413.