Linije tangenti na četiri trokuta

Original: https://www.math.tamu.edu/~sottile/research/stories/4triangles/index.html

H. Brönnimann, O. Devillers, S. Lazard, i F. Sottile

Razmatramo sljedeće jednostavno geometrijsko pitanje: Koji je maksimalan broj linija koje su tangente na četiri trokuta? (Odnosno, računamo linije koje se susreću s jednim rubom iz svakog trokuta.) Radi jednostavnosti pretpostavljamo da su trokuti u prikladnom općenitom položaju, jer algebarska relaksacija gdje rubove zamjenjujemo potpornim linijama ima samo konačno mnogo rješenja. (Zapravo 162 različita složena rješenja.)

Tražimo maksimalan mogući broj, jer je minimum nula: Ako su četiri trokuta dovoljno udaljena, recimo na četiri ugla vrlo velike sobe, tada neće biti takvih uobičajenih transverzala.

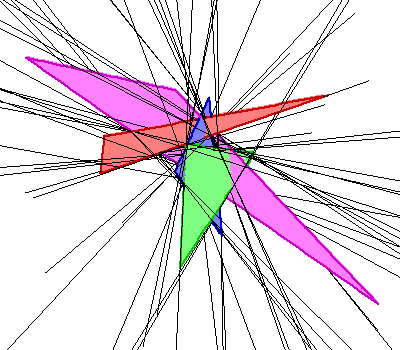
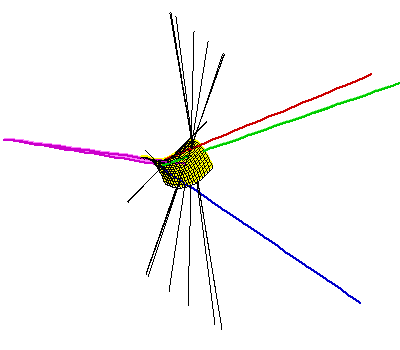
Trenutno je najbolji odgovor na ovo pitanje da je maksimalan broj između 62 i 162, s gornjom granicom 156 ako su trokuti nepodudarni. Gornja granica gotovo sigurno nije najbolja moguća, a također sumnjamo u optimalnost donje granice. Ova donja granica je zbog konstrukcije koju opisujemo na ovoj stranici (povezana sa slikom dolje desno). Ova konstrukcija uključuje narušavanje četiri segmenta linija koji imaju dvije zajedničke transverzale, a svaki od rezultirajućih trokuta ima jedan izuzetno mali kut – prilično su tanki. Naša najbolja konstrukcija koja uključuje četiri masna trokuta ima 40 zajedničkih transverzala. Opis pretraživanja računara pomoću kojeg smo pronašli ovaj primjer povezan je sa slikom dolje lijevo, kao i animacijama.

Ova WWW stranica prati naš članak na ovu temu O broju tangenti linija na četiri trokuta u trodimenzionalnom prostoru.

Slike su povezane sa daljom diskusijom