Original: http://ronney.usc.edu/research/biophysics/BacterialFronts.html
Alison Kraigsley i Paul D. Ronney
Odjel za svemirsku i mašinsku mašinu
Univerzitet Južna Kalifornija, Los Angeles, CA 90089-1453
Steven E. Finkel
Odjeljenje za biološke nauke
Univerzitet Južna Kalifornija, Los Angeles, CA 90089-1340
Sažetak
Iako se mnogo zna o samopromočujućim reakcijskim difuzijskim frontovima koji se javljaju u mnogim kemijski reakcijskim sustavima kao što su plamen, polimerizacijski procesi i neke vodene reakcije, ova velika baza znanja prethodno se nije sustavno primjenjivala na biološke sustave poput širenja pokretnih bakterija. Ciljevi ovog rada su (1) utvrditi da li se takvo znanje može primijeniti na biološke sustave i (2) ako je tako, steći kvantitativnije i prediktivnije razumijevanje bioloških sustava koji pokazuju samopromočujuće fronte. Slijedit će se analogija između širenja pokretnih bakterija i ostalih samopromočujućih fronta s obzirom na dinamička svojstva takvih frontova. Početni eksperimenti s bakterijom E. coli doista pokazuju ponašanje analogno sistemima reakcija-difuzija. Pokušavamo provesti sveobuhvatnu studiju dinamičkih svojstava, uključujući stope širenja, efekte prednje zakrivljenosti, granice gašenja, granice stabilnosti, efekte uzgona, efektivne koeficijente difuzije i vremensku skalu reprodukcije. Te će se informacije upotrijebiti kao ulazi u postojeće analitičke/numeričke modele reakcijsko-difuzijskih fronti i utvrđena valjanost predloženih analogija. Razlike između konvencionalnih reakcijsko-difuzijskih sistema i mikrobioloških sistema takođe će se proceniti. Jedna ključna razlika je da bakterije evoluiraju i reagiraju na stres, faktor koji će se proučavati ponavljanjem navedenog ispitivanja s bakterijama koje su preživjele uvjete gotovo ugasivanja. Ovi podaci će se zatim koristiti za bolje razumijevanje preživljavanja i prilagodbe bakterija u nepovoljnim uvjetima.
UVOD
Reakcijske fronte koje se šire samo u sebi nastaju u mnogim kemijskim i fizičkim sustavima, uključujući plamen, postupke polimerizacije započete slobodnim radikalima i neke vodene reakcije. Sve ove sustave karakteriziraju dvije ključne karakteristike: reaktivni medij (na primjer mješavina goriva i zraka u slučaju plamena) i autokatalizator koji je proizvod reakcije koji također ubrzava reakciju (na primjer toplinska energija u slučaj plamena). Samo-razmnožavanje se događa kada autokatalizator difuzuje u reaktivni medij, pokrećući reakciju i stvarajući više autokatalizatora. To omogućava da se reakciono-difuzijske fronte šire stalnim brzinama daleko od bilo kojeg mjesta iniciranja.
Dva od ključnih karakteristika samoprenosiva reakcija-difuziju frontovima su stopa prostiranja (e) i ograničenje kaljenje. Stopa propagacije je brzina kojom prednjem napredak u reaktivni medij, koji uglavnom ovisi o ukupno vrijeme reakcije skala (τ) i koeficijent difuzije (D) auto katalizatore prema odnosu s ≈ (D/τ)1/2. τ opet ovisi o koncentraciji i aktivnost reaktanata. Granica kaljenje je minimalna ili maksimalna vrijednost nekog parametra (na primjer, minimalno reagensa koncentraciju ili kanal širine) za koje se stalno propagira ispred može postojati. Spojnica koje se javlja između hemijske reakcije i difuznog i konvektivnog transporta u plamenu [[1]], Polimerizacija frontova [[2] ] i vodene reakcije [[3]] dobro shvatio kvantitativno.
Iznenađujuće, analogna linija upit nije primijenjen na mikrobiološke sistema, iako je prvi modeliranje reaktivne-difuzne frontovima, što je dovelo do odnosa s ≈ (D/τ)1/2, je provedena 1937. godine u kontekstu širenja zaraznih bolesti (vidi [[4]]). Svrha našeg istraživanja je da se proceni izvodljivosti tome i iz ovog razviti više kvantitativno razumijevanje takve mikrobiološke sistema. Većina mikrobiološke studije fokusiraju na pojedinačne bakterije i brojanje ponašanje pojedinaca. U ovoj studiji primjenjujemo termodinamičkih zakona i proučavati agregata ponašanje velikog broja pojedinaca. Test slučaj biramo da se fokusiramo na ovoj studiji je vrlo čest i široko studirao Escherichia coli bakterije, a pokretljive bakterije koja (kao i mnogi drugi) pliva pomoću svoje pipke ili flagella u hranjivoj podlozi, dok često mijenja pravac tražiti područja visokog nutrijenata koncentracije. Naime bakterija ima dva načina ponašanja: “run” mod u kojem svoje flagella rotiranje da ga pokrenuti na više ili manje ravnoj liniji, a “sušenje” modu gdje flagella jer je promjenu orijentacije sa malo neto kretanja [[5]]. Rezultirajući kretanje je donekle analogan slučajnog hoda molekula koji dovodi do klasičnog Fickian difuzije (iako mehanizam je potpuno drugačija, jer, za razliku od molekula bakterije prijedlog nije vezan za elastični sudari između bakterija). Također, u povoljnom nutrijenata gradijent, bakterije radi više nego što tumbles, što dovodi do većeg D, dok je u nepovoljnim gradijentima, to tumbles više, što joj je omogućilo da traga za novim pravcima i rezultiralo nižim D; ovo također dovodi do pristran slučajnim hoda da usluge migracije u područjima povećane nutrijenata nivoa.
Ove karakteristike pokretnih bakterija mogu se iskoristiti za modeliranje njihovog ponašanja kao reakcijsko-difuzijske fronte. Brzina (s) širenja od E. coli izmjerili smo (vidi odjeljak Preliminarni rezultati) u agar mediju od 0,3% oko 4,5 mm/h. Vremenska skala (τ) reprodukcije E. coli je oko 20 min. Od brzine širenja s ≈ (D/τ)1/2, D ≈ s2τ, na taj način D ≈ 1.5 x 10-5 cm2/sec. Ova vrijednost je u skladu s očekivanom vrijednošću koja se temelji na kinetičkoj teoriji molekula koja pokazuje da je D proporcionalna brzini čestice (c) pomnoženo sa srednjim slobodnim putem čestice (λ), tj., u slučaju molekula udaljenost koju se čestice kreću prije sudaranja jedna s drugom ili, u slučaju pokretnih bakterija, mijenjanje smjera. l mogu se procijeniti kao c pomnoženo s vremenom (t) bakterije plivaju bez promjene smjera. Za E. coli, an average swimming speed of 21 µm/s, with 21 changes in direction per 30 seconds has been measured. This implies ≈ 1.4 s i l ≈ 3.0 x 10-3 cm and, thus the effective diffusivity D ≈ 6.3 x 10-6 cm2/s, which is of the same order of magnitude as the value of D inferred from D ≈ s2τ.
Zaključujemo da je razumno okarakterizirati širenje pokretnih bakterija kao fronte s difuzijskom reakcijom. Mnoge mikrobiološke studije mjere reakciju sistema na gradijent temperature ili hranjivih sastojaka koji se nameću sistemu; namjeravamo pokazati da bakterije mogu stvarati vlastite gradijente i na taj način se mogu samostalno razmnožavati. Tablica 1 prikazuje predloženu analogiju između plamena (tipičan reakcijski-difuzijski front) i mikrobioloških sistema.
|
Plamen ili molekularno svojstvo
|
Mikrobiološki ekvivalent
|
|
Temperatura
|
Koncentracija bakterija
|
|
Gorivo
|
Hranjive materije
|
|
Difuznost topline ≈ cλ
|
Difuznost bakterija
|
|
Difuzivnost goriva
|
Difuznost hranljivih sastojaka
|
|
Brzina zvuka (c)
|
Brzina plivanja bakterija u “trčati” režimu
|
|
Srednja slobodna staza (λ)
|
c pomnoženo sa prosječnim vremenom za prelazak iz režima rada u režim prevrtanja i natrag
|
|
Vremenski raspon reakcija (τ)
|
Vrijeme reprodukcije
|
|
Gubitak topline
|
Smrt (od pojedinačnih bakterija)
|
|
Gašenje
|
Smrt (svih bakterija)
|
|
Tabela 1. Predložena analogija između plamena i mikrobioloških fronta
|
Komplicirajući faktor plamena, kao i pokretne bakterije, je da se efektivni koeficijent difuzije mijenja s koncentracijom proizvoda. U slučaju plamena proizvodnja proizvoda vodi do veće temperature koja povećava D u gotovo svim slučajevima. U slučaju pokretnih bakterija dobro je poznato da bakterije troše manje vremena u režimu “trčanja”, a više u režimu “prevrtanja” kada je koncentracija hranjivih sastojaka visoka (zašto se osvrnuti okolo kada je trava već zelena?) znači da će srednja vrijednost slobodnog puta l biti niža i samim tim će efektivna difuzivnost biti manja kada je koncentracija hranjivih sastojaka visoka. U slučaju razmnožavajućeg fronta, nekoliko bakterija na prednjem rubu fronta vide visoku koncentraciju hranjivih sastojaka i stoga imaju nisku D. Veće koncentracije bakterija (“produkt” reakcije) na prednjem rubu fronte će postojati u medijum s nižom koncentracijom hranjivih sastojaka i na taj način će se „manje“ odvijati i manje „propadati“, povećavajući l i tako će se D povećavati. Stoga je analogija sa plamenom razumno široka.
Preliminarni rezultati
Gornja rasprava ohrabrila nas je da provedemo preliminarne eksperimente kako bismo testirali održivost naših prijedloga. Ovi su eksperimenti provedeni na 37°C u standardnim petrijevim pločama koristeći hranjivu podlogu na bazi vode koja se sastoji od (osim ako nije drugačije naznačeno) 1% NaCl, 1% triptona, 0,5% kvasca i 0,1% agara. Agar povećava viskoznost medija i u suštini sprečava svako veliko kretanje. Medij je inokuliran bakterijama u točki (obično u središtu posude) i rezultirajući napredak (ako postoji) prednjeg dijela bakterija vidljiv je. Ispitano je nekoliko sojeva E. coli. Nakon početnog prolaznog stanja, svi su pokazali linearno povećanje prednjeg radijusa sa vremenom. Primjer je prikazan na slici 1.
Slika 1 pokazuje da je prednji napredak sporije u početku kada je ispred radijus je mala i prednje zakrivljenosti. Svi ostali testovi su pokazali taj isti trend. Ovo ponašanje se posmatra u hemijskim frontovima u kojem je autokatalitičkog proizvod ima manju difuzivnost nego reaktanata (npr., u slučaju plamena, visoku termalnu difuzivnost i nizak difuzivnost goriva), a razlozi su dobro razumio [[6]]. Dok je difuzivnost u Tryptone nutrijentima je nepoznat, po analogiji sa sličnim molekulama vrijednosti od 10-7 cm2/s može se procijeniti, što je manje nego što su difuzivnost E. coli prema procjeni gore. Shodno tome, ponašanje je prikazano na slici. 1 je u skladu s modelom reakcija-difuziju prostiranje. Osim toga, teorija plamen pokazuje da ako je previše razlikuje od vrijednosti 1, više ili smanjiti odnos proizvoda reaktanta diffusivities, razne vrste ispred nestabilnosti može dovesti. Formiranje obrazac u mikrobiološkim sistemima je dobro poznata [[7]], ali teorija reakcija-difuziju se ne koristi za kvantifikaciju i predvidjeti takve obrasce. Mi ćemo istražiti takve nestabilnosti variranjem medij difuzivnost kroz agar koncentracije. Osim toga, mi sumnjamo da je ovaj izbor vremena run-sušenje od E. coli nije slučajno jer utiče D; ako je D je prenizak ili previsok, nestabilnosti rezultat koji može biti nepovoljna za opstanak. Mi ćemo nastaviti ovaj pojam ispitivanjem efekta agara koncentracije o vremenu brzine i trčanje-pad bakterija pod mikroskopom i utvrditi da li je bakterija prilagođava (ili u hodu, ili evolucijski procesi) njegova brzina i run-sušenje vremena promijeniti svoje efikasne D održavanje stabilnog frontova.
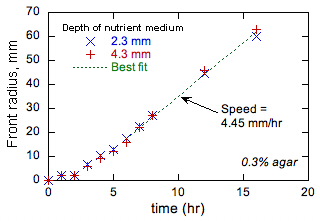
Slika 1. Primjeri eksperimentalnih podataka o prednjim radijusima bakterija kao funkcija vremena.
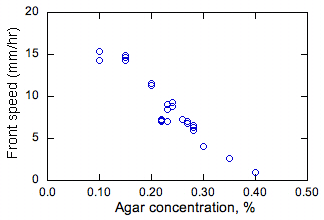
Slika 2. Izmjereni učinak dubine agara i otopine na stalne brzine razmnožavanja bakterijskih fronti.
Učinak koncentracije agara i dubine hranjivog medija na stalne vrijednosti brzine razmnožavanja s prikazan je na slici 2. Pri 0,5% ili većoj koncentraciji agara (nije prikazano) medij je u osnovi bio čvrst i bakterije su se širile samo na površini medija, a ne u rasutom stanju. Difuzijsko ponašanje bakterija u ovom slučaju nije vjerovatno jer ne mogu plivati. Pri 0,4% i nižoj koncentraciji agara, bakterije se šire putem medijuma. Primjećene su najveće stope razmnožavanja pri najnižim koncentracijama agara (a vreme i najniža viskoznost medija). To se očekuje budući da pri nižoj viskoznosti bakterija može plivati brže i stoga bi trebala imati viši efektivni D, što dovodi do većeg s (obzirom da je s proporcionalan D1/2 kao što je gore spomenuto).
Otkriveno je da dubina rastvora gotovo da i nema uticaja na s. Uzimanjem poprečnih presjeka medija nakon djelomičnog širenja fronte, utvrđeno je da su frontovi uglavnom u vertikalnoj dimenziji jednolični. Stoga protok plovnosti ne utječe na ove prednje strane, u protivnom se može očekivati utjecaj dubine otopine na s, ili nejednakosti u okomitom smjeru. Budući da su ispitivanja provedena u zraku, ova opažanja također pokazuju da difuzija kisika u medij nije značajna, jer bi u suprotnom rast blizu površine hranjive otopine bio različit od onog ispod površine. Ovaj posljednji rezultat pokazuje da bakterije rastu anaerobno.
Kako bi se utvrdilo postoje li granice “gašenja” na bakterijskim frontovima, proveden je eksperiment u kojem su bakterijske fronte pokušale razmnožavati kroz uske i široke kanale sa zidovima antibiotika. Budući da antibiotici uklanjaju autokatalitički proizvod (bakterije), efekat zidova analogan je gubicima topline hladnim zidovima u plamenu. Za prednje širenje u uskim kanalima dobro je poznato da granica gašenja dolazi zbog gubitaka topline na stijenkama kanala kada je Peclet broj Pe = sw/D, gdje je w širina kanala, a D difuzivnost, manja od a kritična vrijednost. Dakle, uz prisustvo gubitaka topline, fronte se mogu širiti širokim kanalima (visoki Pe), ali ne uskim kanalima (nizak Pe). Slika 3 pokazuje da se fronte mogu širiti širokim kanalom, ali ne i uskim kanalom, što ukazuje na granicu gašenja. U ovom radu će se testirati primjenjivost odnosa kaljenja Pe = sW/D = konstanta na granici.
Ispitan je i učinak koncentracije hranljivih sastojaka triptona; utvrđeno je da se na polovici nominalne vrijednosti neće dogoditi širenje, dok je s gotovo nepromijenjen udvostručenjem koncentracije triptona s njegove nominalne vrijednosti. Ovo može ukazivati na granicu gašenja, čak i ako nema antibiotskih zidova. Analogno ponašanje se događa u plamenu zbog radijativnih gubitaka topline kada je koncentracija goriva preniska. Istražit ćemo ovu granicu bez zida i pokušati utvrditi mehanizam gubitaka koji je odgovoran za suzbijanje širenja fronta na niskim razinama hranjivih sastojaka.
Titriranje medija za dobivanje broja bakterija dosljedno je pokazalo značajan vrhunac koncentracije bakterija na vodećem pročelju, praćen velikim padom ispred i, kasnije, drugi vrh daleko iza prvog. To je u skladu sa slikama prikazanim na slici 3. U budućem radu koristit ćemo se analizom titriranja kako bismo utvrdili da li je debljina fronte ≈ D/s kako je teorijski predvidjelo. Na osnovu vizualnog pregleda s slike 3, debljina prednje strane je oko 1 mm, što je blizu predviđanja D/s = (1.5 x 10-3 mm2/sec)/(4.5 mm/hr) = 1.2 mm. Rezultati s divljim sojem bakterija pokazali su nešto brži početni prolazni i kraći put i udaljenost da bi se postigla stalna stopa razmnožavanja u odnosu na genetski obilježene sojeve.
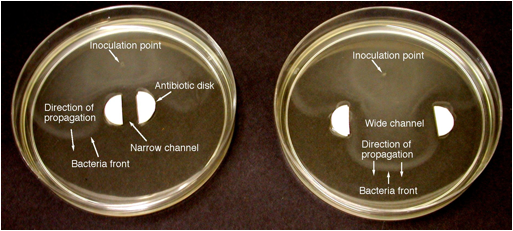
Slika 3. Fotografije fronti pokretne bakterije E. coli koja se razmnožava uskim (6 mm, lijevo) i širokim (35 mm, desno) kanalima sa bočnim zidovima antibiotika Kanamycin (100 mikrolitara Kanamycina po strani), snimljenim 6,5 sati nakon inokulacije. Oba slučaja: 2086 divlji soj E. coli, 0,1% agar, standardni hranjivi medij.
Aktuelni istraživački program
Na temelju očiglednog uspjeha reakcijsko-difuzijskog modela u opisivanju ovih preliminarnih eksperimentalnih rezultata, mi slijedimo sljedeći istraživački program:
- Odredite stope razmnožavanje E. coli frontova u funkciji nutrijenata koncentracije, srednje motilitet (kroz mijenja agar koncentracija), temperatura, koncentracija ambijentalne kisika (aerobik vs. anaerobni okoliš), a debljina sloja hranljive podloge. Ovi testovi će biti izvedena na isti način kao i preliminarni eksperimenti gore opisano. Osim toga, da se poboljša vizualizaciju frontova, koristit ćemo E. coli specifične fluorescentnih boja iz Molecular Sonde, Inc (Eugene, OR). poboljšati vizualizaciju frontova. Ultraljubičasti izvor svjetlosti (kupuje) ili Ar-ion laser će se koristiti za pobuđuju fluorescentnih boja.
- Odrediti D zasnovan na relaciji D ≈ s2τ i usporedite s tim očekuje na osnovu relacija D = c2τ, gdje je c mjeriti (pomoću video mikroskopija) brzina (c) i znaci vremena za promenu pravca. Standard video je adekvatan od vremena skali run-sušenje je obično 1 sekunde, a stopa video kadriranje je 30 u sekundi.
- Odredite granice kaljenje i ograničenje Péclet brojevi dozvoljavajući fronta s propagandom kroz kanale različite širine (w) koji imaju antibiotske zidove (Kanamicin ili slično) i utvrditi da li Pe je konstantna na granici, odnosno, je stopa prostiranja (s) na ograničenje proporcionalna 1/w?
- Odredite granice kaljenje u nedostatku zidova (smanjivanjem nutrijentima koncentracije, za različite agar koncentracije) i utvrditi mehanizam gubitka (tj. Mehanizam smrti ćelija) odgovoran za to ograničenje.
- Odredite granice stabilnosti kao funkcija odnosa proizvoda (bakterija) u reagensa (nutrijenata) difuzivnost variranjem agar koncentracije u hranljive podloge i koncentraciju hranljivih materija. Fluorescentnih bojila će olakšati snimanje neuniformna frontovima i formiranje obrasca.
- Utvrdite da li postoji plovnost uticaj na prostiranje. Od E. coli bakterije imaju gustoću malo drugačiji od vode, na niske viskoznosti će doći do efekta uzgona. Većina istražitelji koriste visoke viskoznosti agara za sprečavanje fluida, ali mnogi pravi E. coli sredinama imaju vodu poput viskoznosti. Efekti plovnost će biti saslušani testiranjem prostiranje u medijima bez agara u vertikalnom paralelno ploča aparata (koji se naziva “Hele-Shaw” ćelije u mehanici fluida literaturi) i da će se pridržavati prednji obrazac i razmnožavanje stopa.
- Model ove rezultate uz pomoć naših postojećih analitičkih/numeričkih modela reakcija-difuzije frontovima.
Naravno, postoje i neke razlike između konvencionalnih reakcijsko-difuzijskih sistema i mikrobioloških sistema. Jedna ključna razlika je da bakterije evoluiraju i reagiraju na stres, faktor koji će se proučavati ponavljanjem navedenog ispitivanja s „iskusnim“ bakterijama koje su preživjele uvjete gotovo ugasivanja. Druga razlika, kao što je diskutirano gore, su pristrana difuzijska svojstva. Ova pristranost može se modelirati korištenjem nelinearne difuzione veze da zamijeni Fikov zakon.
PRAKTIČNA VAŽNOST
Ovaj rad je istraživanje dinamike nove klase razmnožavanja fronta koje uključuju pokretne bakterije. Studija dinamike fronta ima brojne primjene kao što je gore raspravljano. Ove su studije, međutim, od posebnog interesa za mikrobiologe jer se odnose na mehanizme dugoročnog preživljavanja i evolucije koje koriste bakterije. Jedan od glavnih faktora koji utječu na brzinu evolucijske promjene u tim bakterijskim sustavima jesu nivoi stresa u okolišu, kao i prijelaz iz jednog okruženja u drugo. Sustavi kulture koje razvijamo predstavljaju nova okruženja u kojima ta pitanja evolucije i preživljavanja nisu riješena. Ovaj rad daje prvi pokušaj, prema našim saznanjima, biofizički okarakterizirati ove efekte.
Posebno je zanimljivo proučavanje uzgoja E. coli u anaerobnim uslovima. Kad E. coli (i sve druge enteričke bakterije) rastu u vezi s ljudskim probavnim traktom, one rastu u anaerobnim uvjetima. Želimo početi proučavati reakcije bakterijskog stresa u nedostatku kisika kako bismo dodatno proširili naše opće razumijevanje kako se ova bakterija prilagođava životu u širokim raznim nišama u okolišu. Na primjer, trenutno nije poznato djeluju li mehanizmi popravljanja i mutacije oštećenja DNK koje je prof. Finkel proučavao (i za koje se pokazalo da su važni za prilagodbu na nova okruženja) u anaerobnim uvjetima. Ove će studije premostiti jaz od osnovnih istraživanja u medicinski relevantnijim područjima.
Reference
[1]. Williams, F. A., Combustion Theory, 2nd Ed., Benjamin-Cummins, 1985.
[2]. Pojman, J. A., Hyashenko, V. M., Khan, A. M., “Free-radical frontal polymerization: self-propagating reaction waves.” J. Chem. Soc., Faraday Trans. 92, 2825 (1996).
[3]. Epstein, I. R. Pojman, J. A. An introduction to nonlinear chemical dynamics, Oxford, 1998.
[4]. Winfree, A.T., The Geometry of Biological Time, Springer-Verlag, 1990; Murray, J.D., Mathematical Biology, Springer-Verlag, 1993.
[5]. Berg, H. C., “Motile Behavior of Bacteria” Phys. Today 53, 24 (2000).
[6]. Lewis, B., von Elbe, G., Combustion, Flames, and Explosions of Gases, 3rd ed., Academic Press, 1987.
[7]. Budrene E.O., Berg H. C., “Complex patterns formed by motile cells of E. coli,” Nature 349, 630 (1991).



